Trio formado por dois físicos e um matemático desenvolveu nova metodologia para resolver um dos 23 problemas propostos pelo matemático alemão David Hilbert em 1900. Se confirmada, resposta tem o potencial de impactar áreas como ecologia, engenharia e computação, ao aumentar a precisão das previsões de sistemas dinâmicos

Malena Stariolo – Jornal da Unesp – “Quem de nós não ficaria feliz em levantar o véu atrás do qual o futuro está oculto; lançar um olhar sobre os próximos avanços de nossa ciência e sobre os segredos de seu desenvolvimento nos séculos vindouros?” Com esse questionamento, o matemático alemão David Hilbert iniciou sua palestra de abertura do Congresso Internacional de Matemáticos de 1900, realizado em Paris. Durante sua fala, Hilbert passeou pela história da matemática para apresentar uma lista de 23 problemas desenvolvidos por ele e que ainda estavam sem solução. O matemático acreditava que a busca pelas respostas e reflexões em cima desses postulados iria nortear os avanços da física e da matemática no próximo século.

Passados 124 anos, a maioria dos Problemas de Hilbert foi parcial ou totalmente solucionada. A exceção fica por conta dos problemas 8, 13 e 16, que seguem suscitando esforços de especialistas ao redor do mundo. O problema 16, chamado “Problema da topologia de curvas e superfícies algébricas”, é dividido em duas partes e cobre o encontro da álgebra e da geometria na matemática; solucioná-lo permitiria gerar aplicações em áreas como ecologia, engenharia e computação quântica. Sua história, entretanto, tem sido conturbada. No passado, vários pesquisadores acreditam ter encontrado uma solução adequada. No entanto, nenhuma das propostas foi considerada válida pela comunidade dos matemáticos, culminando, inclusive, na retirada de um artigo publicado, em 2004, na revista científica Nonlinear Analysis.

Duas décadas após esse evento, pesquisadores da Unesp acreditam que finalmente foram capazes de encontrar uma resposta definitiva para a questão. A solução foi proposta por Vinícius Barros da Silva, por seu orientador no curso de doutorado em Física Aplicada pela Unesp, Edson Denis Leonel e pelo matemático João Peres Vieira. Leonel e Vieira são docentes dos Departamentos de Física e Matemática do Instituto de Geociências e Ciências Exatas da Unesp, campus de Rio Claro. O trio apresenta suas ideia no artigo “Exploring Limit Cycles of Differential Equations through Information Geometry Unveils the Solution to Hilbert’s 16th Problem”, publicado na revista Entropy. No texto, Vinícius Barros da Silva relata como olhou para o problema a partir do seu conhecimento em física, o que permitiu uma abordagem inovadora sobre a questão e culminou no desenvolvimento de uma nova metodologia, chamada Teoria Geométrica de Bifurcações.

“A principal motivação para investigar esse problema foi, em primeiro lugar, o desafio, já que muitos matemáticos e físicos não conseguiram encontrar uma resposta”, diz Silva. “Acho que isso se deve em parte ao fato de que as abordagens anteriores não atacavam o problema diretamente, e algumas traziam uma versão simplificada da questão”, diz.

A pergunta em aberto

A questão apresentada no 16^o Problema de Hilbert envolve determinar o número máximo de “ciclos limites” em expressões matemáticas que são usadas para descrever como determinados fenômenos variam ao longo do tempo, chamadas equações diferenciais polinomiais. Essas equações podem ser aplicadas, por exemplo, para gerar previsões sobre como uma população de animais irá mudar ao longo do tempo.

Já os ciclos limites são padrões repetitivos que aparecem nas soluções dessas equações. Utilizando as mudanças de populações de animais como exemplo, os ciclos limites representam os padrões ou seja, a repetição de determinadas tendências. Tomemos por base o exemplo das populações de animais para explicar o conceito. Em um ambiente de floresta em que convivem presas e predadores, ao aumento de uma população de presas segue-se o crescimento no número de predadores. A ação de um número maior de predadores resulta numa queda na população de presas e, consequentemente, em uma queda na população de predadores, o que enseja, novamente, um novo aumento na população de presas.

De maneira simplificada, o trio de pesquisadores conseguiu resolver a pergunta de como seria possível prever quantos tipos diferentes de padrões (ou ciclos) poderiam aparecer nessa floresta antes que ela entrasse em uma rotina, ou seja, antes que as mudanças passassem a se repetir sempre da mesma forma. Esse comportamento, que tende a uma rotina após alguns ciclos de mudança, já foi bastante observado por físicos em diferentes sistemas, que vão desde escalas atômicas até meteorológicas. Mas, embora o fenômeno fosse bastante familiar aos pesquisadores, até agora não existiam descrições matemáticas que explicassem e trouxessem mais informações sobre esse tipo de funcionamento.

Um novo olhar para o problema

Até então, todas as tentativas de resolução do problema eram feitas a partir dos mesmos métodos matemáticos. Para Silva, esse fator dificultou a busca por respostas. Segundo o físico, as principais abordagens estavam divididas entre a utilização de teoremas negativos e os métodos aproximativos. “O grande problema com essa abordagem é que, no caso dos teoremas negativos, eles são muito bons para identificar quando o sistema não tem um ciclo limite, mas ele não fornece nenhuma informação além disso. Esses teoremas nos permitem descobrir apenas se há ou não um ciclo limite, mas quantos são? Não temos como saber”, diz. A problemática da segunda abordagem está na simplificação do problema, porque pode ser utilizada apenas para encontrar o número mínimo de ciclos limites. Entretanto, o problema de Hilbert busca uma resposta para o número máximo.

O pulo do gato para o grupo veio ao tentar abordar o problema a partir da geometria. Os pesquisadores utilizaram um método chamado geometria de informação de Fisher, que permite gerar um mapa que mede as “distâncias” entre diferentes estados de um sistema – como os momentos em que há mais ou menos predadores e presas. A visualização dessas distâncias gera um tipo específico de curva e, a partir de simulações em diferentes sistemas, o grupo percebeu que a resposta para o número de ciclos limites estava contida na curvatura gerada nesse mapa.

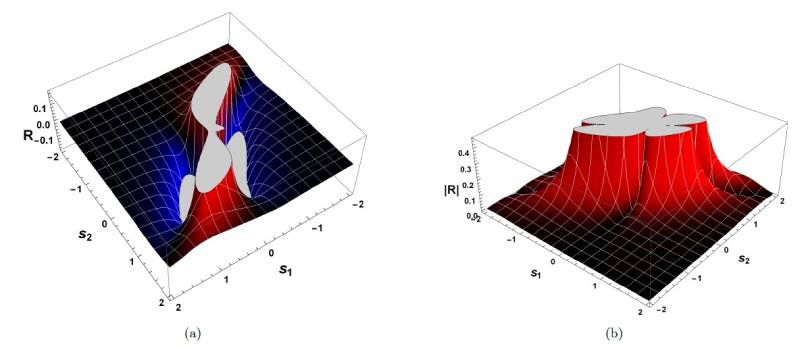
“Identificamos que quando um sistema não tinha um ciclo limite, a curvatura era zero ou negativa; quando existia apenas um ciclo limite; a curvatura era positiva e se tornava infinita em pontos simétricos em relação à origem do sistema; agora, quando o sistema tinha mais de um ciclo limite, a curvatura divergia em pontos diferentes, não simétricos”, diz Silva. Cada um desses pontos, presentes na curva e que determinam o caminho que o sistema irá seguir, correspondem a um ciclo limite. Com essa visualização, o grupo percebeu que era capaz não apenas de identificar quantos ciclos limites um determinado sistema tem, mas também onde eles estão posicionados no espaço, contribuindo para a solução do problema. O grupo apelidou essa nova abordagem de Teoria Geométrica de Bifurcações.

Ao saber em que momentos um sistema “muda”, e a partir de quando essas mudanças começam a se repetir, é possível gerar previsões mais precisas sobre o futuro de um sistema, o que possibilita planejar com antecedência determinadas ações com base nesse conhecimento. Por isso, a solução proposta pelos pesquisadores da Unesp pode gerar importantes implicações no estudo de sistemas complexos e dinâmicos, em áreas como biologia, física, engenharia, meteorologia e computação, entre outras.

Na meteorologia, por exemplo, ela pode auxiliar na previsão de eventos como El Niño e La Niña, que são fenômenos que influenciam temperaturas globais, padrões de chuvas e secas, e a intensidade de furacões, com ciclos que variam de 3 a 7 anos. Saber quantos ciclos limites podem existir nesse sistema climático nos ajudaria a prever de maneira mais acertada quantas vezes e com que frequência esses fenômenos podem ocorrer, além de identificar a possibilidade do surgimento de novos padrões desconhecidos.

A importância de uma perspectiva multidisciplinar

O primeiro contato de Silva com o problema se deu durante uma reunião com seu orientador, Leonel. Na ocasião, o professor escreveu o problema e convidou o estudante a pensar a respeito. “Eu lembro do dia em que ele chegou no grupo para conversarmos. Apresentei o problema na lousa e ele ficou analisando, pareceu ter ficado encantado. Logo aceitou trabalhar nele”, conta Leonel.

Embora a dupla de físicos alcançasse uma compreensão extensa dos fenômenos que o problema descrevia, ainda faltava a elaboração de uma descrição matemática, um elemento essencial para garantir a robustez da pesquisa que estavam conduzindo. Foi da necessidade de elaborar esta descrição que surgiu o convite para que o matemático e docente Vieira integrasse o grupo. Sua chegada concretizou a união entre as áreas da física e da matemática propriamente dita. “O físico é um cientista muito prático. Ele faz observações e anota o que está acontecendo. Mas o matemático busca o rigor matemático. Isso irá garantir a validez do resultado, e trará maior robustez à pesquisa”, diz Vieira.

O trio sustenta que a ciência de qualidade deriva da colaboração entre os diferentes campos científicos. E a oportunidade de decifrar um enigma proposto há mais de um século só reforçou essa percepção. “A parceria entre pesquisadores de diferentes áreas é saudável e fantástica porque, enquanto físicos, não temos a formação para fazer análises estatísticas tão profundas. Sem a contribuição da matemática, provavelmente não teríamos chegado tão longe no problema”, diz Leonel.

“Percebo que essa sinergia entre física e matemática foi fundamental. E essa parceria pode mostrar que nós, aqui na Unesp, também conduzimos pesquisa na fronteira do conhecimento. Também temos o potencial necessário para fazer contribuições importantes para a física, para a matemática e para o mundo ao nosso redor”, diz Silva.